Функцијата на објективот е двострана: да собира што е можно повеќе светлина и да овозможи набљудување на објектот под што е можно поголем агол.
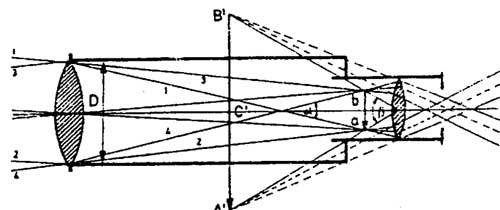
Што повеќе се собира светлина тоа значи дека може да се набљудуваат послаби тела, според тоа јасно е дека колку е поголем објективот толку е подобар од причина што има поголема површина.
Ако земеме дека дијаметарот на зеницата кај човековото око кога е отворена, значи навикната на темно, е 7mm (всушност оваа бројка варира од човек до човек и се движи во границите од 6 mm до 8 mm) тогаш објектив со дијаметар D милиметри собира онолку пати повеќе светлина колку што неговата површина е поголема од површината на зеницата на човековото око, па според тоа ќе имаме:
S = (D / 7)2
S се нарекува светлосна моќ на телескопот.
Пример:
Да се пресмета светлосната моќ кај телескоп со апература од 200 mm
S = (200/7)2 = 816
Со помош на светлосната моќ можеме ја да одредиме и јачината на ѕвездите кои можеме да ги набљудуваме со помош на телескопот. Ако телескопот собира S пати повеќе светлина од голото око, тогаш со него можеме да гледаме и S пати потемни тела. Со голо око можеме да гледаме тела со магнитуда од околу 6 зведени величини, со помош на фотометриски формули се доаѓа до следното:
mg = 6 + 2,5*log(S)
Пример:
Да се најде граничната ѕвездена магнитуда на телескоп со објектив од 200 mm
mg = 6 + 2,5*log(816) = 13,3
Со вршење на набљудувања со повеќе телескопи е покажано дека граничната ѕвездена магнитуда се достигнува само при ведри, темни ноќи без месечина. При многу добри услови можно е да се набљудуваат и магнитуди потемни за една ѕвездена магнитуда од оние добиени во горната равенка. Тука голема улога игра и оптичкиот квалитет на објективот како и набљудувачкото искуство на астрономот.
Доколку во равенката за гранична ѕвездена магнитуда на местото на S се вметне изразот со дијаметарот на објективот тогаш добиваме друг облик на равенката за гранична ѕвездена магнитуда кој се користи многу често:
mg = 6 + 5*log(D / 7) = 1,8 + 5*log(D)
Друга важна величина кај телескопите е зголемувањето. Зголемувајќи ги набесните тела телескопот ни овозможува на нив да уочуваме многу поситни детали отколку со голо око. Зголемувањето (P) претставува однос помеѓу фокусното растојание на објективот (F) и фокусното растојание на окуларот (f):
P = F / f
Зголемувањето не може да се менува во произволни граници. Ако зголемувањето е премало, доаѓа до губење на светлост така да телескопот не е целосно искористен. Додека пак ако зголемувањето е премногу големо добиваме темни размачкани слики без детали, и ќе ги истакнеме несовршеностите на оптиката и треперењето на зраците. Границите во кои што може да се движи зголемувањето на еден телескоп зависи од неговиот објектив, од неговиот тип и квалитет. Но најчесто објективите се со задоволувачки квалитет, така да квлитетот на ликата го ограничуваат оптичките закони (дифракцијата) како и треперењето на зраците.
Зголемувањата можат да се поделат на мали, средни и големи.
Малите зголемувања даваат светла слика со многу големо видно поле и затоа се користат за барање на објекти на небото, за набљудување на комети, на маглини и сл. Кај малите зголемувања треперењето на зраците не делува на квалитетот на сликата.
Средните зголемувања се користат за набљудување на Месечината и планетите, потоа за двојни ѕвезди, за посјајни маглинии сл. Треперењето на зраците се приметува само ако е изразито големо.
Големите зголемувања се користат исто како и средните за планетите, за Месечината , за двојни ѕвезди ако атмосферата е доволно мирна. Кај овие зголемувања видното поле е многу мало, сликата темна и многу осетлива на треперењето на зраците.
Границите помеѓу поедините зголемувања не се многу остри но сепак може да се одредат според следните формули:
премалите зголемувања се помали од:
Pmin = D(mm) / 7
малите зголемувања се помеѓу Pmin и Ps
Ps = D(mm) / 3
тука спаѓа и тн. нормално зголемување
Pn = D(mm) / 5
средните зголемувања се наоѓаат измеѓу Ps и Pv
Pv = D(mm)
над Pv се движат големите зголемувања и се движат се до Pmax
Pmax = 2,5*D(mm)
Зголемувањата над Pmax се преголеми, со многу темни слики и многу матни. Како што се заприметува овие зголемувања зависат само од дијаметарот на објективот. Односно зависат од светлосната моќ на објективот, колкава светлина тој може да собере, а со тоа да ни даде и почиста и појасна слика на објектот што го набљудуваме.
Пример:
Да се најдат корисните зголемувања за објектив со дијаметар од 200 mm:
Pmin = 200 / 7 = 29 x
Pn = 200 / 5 = 40 x
Ps = 200 / 3 = 67 x
Pn = 200 = 200 x
Pmax = 2,5*200 = 500 x
Законите за физиката ја ограничуваат острината на сликата која може да се добие со објектив со одреден дијаметар, така што за набљудување на поситни детали треба да користиме поголеми објективи.
Најмалото аглово растојание помеѓу две ѕвезди со ист сјај, кои се уште може да се раздвојуваат помеѓу себе, со помош на телескоп кој има објектив со дијаметар D, е дадено со следнава равенка:
R(²) = 120 / D (mm)
каде што R е агловото растојание мерено во аглови секунди. Ако ѕвездите не се со ист сјај, тогаш растојанието кое се уште може да се раздвои помеѓу овие ѕвезди расте со растењето на разликата во сјајот помеѓу ѕвездите. Многу често раздвојувањето на деталите кај тела со ист или сличен сјај, како на пример деталите, на една планета е многу полошо од она предвидено со горната равенка.
Пример:
Да се одреди раздвојната моќ на телескоп со објектив од 200 mm
R = 120 / 200 = 0,6²
ОКУЛАРИ
Има четири основни типови окулари:
1. класични леќи
2.хајгенсов тип окулари
3.рамсденов окулар
4.симетрични окулари
класични леќи
Ова се обично планконвексни леќи и се користат за големи зголемувања. Најдобро работи кај телескопи со голем F број, на пример кај рефракторите. Недостаток им е малото видно поле кое се движи од 15 до 25 степени. Кај овие окулари рамната страна се мести од напред.
хајгенсов окулар
Се состои од две планковексни леќи. Тој е изработен на принципот според кој комбинацијата на две леќи, изработени од ист тип стакло, е ахроматична доколку тие две леќи се оддалечени една од друга за половина од збирот на нивните фокусни далечини. Доклку нивните фокусни далечини се F1 и F2 тогаш ахроматична леќа ќе добиеме доколку тие се оддалечени една од друга за: d = (F1 + F2) / 2.
Окуларот така се монтира да помалата леќа дојде поблиску до окото. Хајгенсовиот окулар има широко видно поле, понекогаш и до 50 степени. Се користи кај телескопи со F над 10 (кај помалите се јавува аберација), најдобро работи кај рефрактори.
рамсденов окулар
И овој окулар како и хајгенсовиот работи на принципот на ахромација. Тој се состои од две исти планковексни леќи свртени една кон друга со испапчените страни.
Меѓусебното растојание треба да им биде 2/3 до 3/4 од фокусното растојание не една од леќите. Видното поле е некаде околу 30 степени и е добар како трагач. Може да се користи и на рефлектори со F до 7 или 6.
симетрични окулари
Со доближување на два ахроматични окулари со испапчените страни блиску еден до друг се добива симетричен окулар. Може да се доближат до околу 0,1 – 1 mm но мора да се внимава да не се допрат бидејќи ќе дојде до оштетување на окуларите. Ваков окулар има големо видно поле и до 50 степени и добро работи на телескопи со F до 5 или 4.






