Потрагата по ѕвездена паралакса започнува уште во античка Грција пред новата ера и трае многу долго. Ѕвездената паралакса е значајна како еден од доказите дека Земјата се движи. Со нејзиното мерење се одредува растојанието од Сонцето до ѕвездите, а со одредување на растојанието се отвараат врати за многу други откритија за ѕвездите. Во потрагата по паралакса значаен придонес дале многу научници, математичари, астрономи и инженери од различни временески периоди. Мерењата од првата ѕвездена паралкса се објавени дури во 19тиот век.
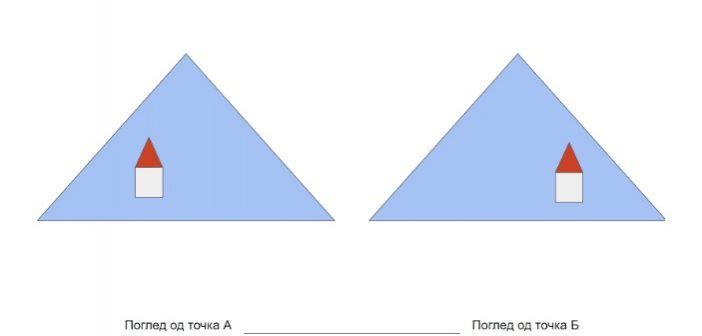
Паралаксата е поместувањето или разликата во привидната положба на објект гледан од две различни точки (локации), и се мери со аголот, односно полуаголот на наклонување помеѓу тие две линии на гледање. Ефектот на паралакса го гледаме постојано. На пример, се наоѓамe на ливада и пред нас гледаме далечна планина и една куќичка. Да речеме дека ливадата е голема и можеме непречно да шетаме низ истата. Ќе пробаме да го видиме ефектот на паралакса користејќи ги планината позади куќата и местоположбата на куќата во однос на планината од позадината. За да го направиме тоа треба да обрнеме внимание на нашата моментална позиција. Погледнуваме кон куќата и внимателно забележуваме каде се наоѓа куќата во однос на планината. Како што е прикажано на Слика 1, од почетната позиција ни изгледа дека куќата се наоѓа на левата страна од планината. После пешачење од неколку метри пак треба внимателно да ја разгледаме позицијата на куќата во однос на планината од позадината. Сега гледаме дека куќата се наоѓа на десната страна од планината. Ние се поместивме неколку метри, но привидно изгледа како и куќата да се поместила. Тоа привидно поместување на куќата е ефектот на паралакса. Планината не се помести (привидно) бидејќи таа е многу подалеку од куќата, што е нашиот предмет на набљудување. Значи, на почетокот, од точка А, куќата изгледа како да се наоѓа на левата страна од планината, а на дистанца од неколку метри куќата изгледа како да се наоѓа на десната страна од планината. Кога се движиме (ја менуваме локацијата на полето од каде набљудуваме) изгледа дека и објектите околу нас се движат. Колку е поблиску објектот што го набљудуваме толку е поголем ефектот на паралакса или привидното поместување.
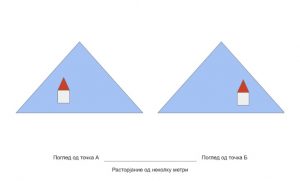
Слика 1
Многу животни, меѓу кои и луѓето имаат две очи чиишто видни полиња се преклопуваат и со тоа преклопување на видно поле всушност се добива ефектот на паралакса или длабинска перцепција. Популарен пример за ова е тестот со прстот и затворање на двете очи едно по едно наизменично. Ставаме еден прст (на пример показалецот) пред нашата глава. Со слободната рака го покриваме едното око. Обрнуваме внимание што точно се наоѓа позади нашиот показалец, тоа може да е дел од кујната, телевизорот, дел од планина итн. Без да го поместуваме показалецот, со слободната рака сега го покриваме другото око. Обрнуваме внимание пак на позадината. Ќе забележиме дека позадината се променила. Ако претходно показалецот се наоѓаше во центарот на телевизорот сега веќе не е така. И ова е ефект на паралакса. Примери за ефекти на паралакса има многу во нашето секојдневие и истиот може да се искористи за да се одреди растојанието од нас до објектот што го набљудуваме, со користење на тригонометарски принципи.
Ефектот на паралакса бил познат уште во времето на античките грци. Аристарх (грчки филозов, кој живеел од 310 до 230 год. п.н.е.) го презентирал првиот познат хелиоцентричен модел, дека Земјата се движи околу Сонцето. Но оваа негова идеја била отфрлена во поглед на геоцентричниот модел поддржан од Аристотел (384 – 322 год. п.н.е.) и Птоломеј (100 – 170 г.). Геоцентризамот останал најпопуларен и прифатен модел меѓу научниците се додека Никола Коперник не ја објавил неговата теорија за хелиоцентризам. Една од причините зошто хелиоцентризмот на Аристарх па подоцна и на Коперник не бил прифатен е заради отсуството на видлив ефект на паралакса на ѕвездите.
Хелиоцентризмот кажува дека Земјата се движи околу сонцето, а тоа значи дека поминува огромен пат. Движењето на Земјата би требало да значи дека треба да можеме да видеме привидно поместување на ѕвездите на небото, но тоа не било така, научниците не забележале менување на положбата на ѕвездите во однос на позадината во текот на целата обиколка околу сонцето (во текот на една година). Тоа што многу од научниците тогаш не го зеле во предвид е дека тие фиксни ѕвезди се на огромни растојанија од Земјата и затоа не се забележува нивното привидното поместување. Ова е во согласност во Евклидовата геометрија, која вели дека ако растојанието до предметот на набљудување е многу големо тогаш паралаксата е незабележлива. Но во тој период растојанијата помеѓу ѕвездите па и големината на самиот универзум била непозната и огромниот празен простор меѓу планетите и ѕвездите бил тешко замислив.
Теоријата за хелиоцентричниот модел, презентирана од античкиот филозоф, математичар и астроном Аристарх, се популаризирала дури во 16 тиот век (околу 2000 години подоцна) со хелиоцентричниот модел претставен од Никола Коперник (1473 – 1543 год.). Како што хелиоцентричниот модел давал поедноставни одговори на големите прашања и подобро се вклопувал со новите мерења и пронајдоци, така почнала и трката за потрагата по ѕвездена паралакса. Привидното движење на ѕвездите, без разлика колку мало би значело потврда дека Земјата навистина се движи. Како што минувале декадите па и вековите, теоријата се повеќе покажувала дека ѕвездената паралакса постои, но потрагата по нејзе сепак била неуспешна. Главниот инструмент за забележување на паралаксата биле човечките очи се додека Галило Галилеј (1564 – 1642 год.) не го свртел телескопот кон небото. Сè поусовршените телескопи ги зголемувале очекувањата, но паралаксата останала не откриена сè до 19ти-от век.
Во 1673, Џовани Касини, успеал да го измери растојанието помеѓу Земјата и Марс, а со тоа и Земјата и Сонцето користејќи го ефектот на паралакса. Тој и неговиот соработник Ричер, извршиле мерења на позицијата на Марс во однос на околните т.н. фиксни ѕвезди во исто време но од различни позиции. За да успешно го детектираат аголот на паралкса, растојанието помеѓу Земјата и Марс треба да биде колку што е можно помало (Марс е во перихел), а растојанието од направените мерења од Земјата треба да е колку што може поголемо (Касини ги направил мерењата од Парис, а Ричер од Француска Гвајана). Касини го испратил неговиот соработник Ричер во Кајена, Француска Гвајана една година пред Марс да биде во опозиција, со инструкции за бројни астрономски мерења. Тој ги направил истите астрономски испитувања во исто време и потоа чекал една година да се врати Ричер со неговите податоци, за да се извршат потребните калкулации. Неговите резултати покажале дека растојанието помеѓу Марс и Земјата е 140 милиони километри, што е само 7% разлика од денешнота официјално прифатена далечина помеѓу Марс и Земјата (150 милиони километри). Со ова за прв пат се дава точна репрезентација за вистинската големина на соларниот систем. Мерењата покажале дека соларниот систем е 20 пати поголем од големината претпоставена од античките грци пред околу 2000 години. Мерењата за паралаксата на Марс се правени врз основа на позадинските т.н. фиксни ѕвезди, истите тие биле основиот аргумент за многу од тогашните астрономи (меѓу кои и Тихо Брахе) за неприфаќање на хелиоцентричниот модел. Ќе поминат уште повеќе од 150 години пред првото официјално забележување на паралакса на ѕвездите блиски до Сонцето.
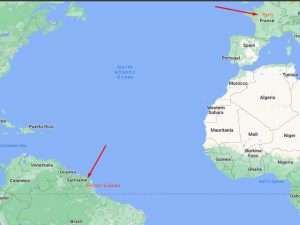
Слика 2
Ѕвездената паралакса, всушност, е истиот ефект на паралакса опишан погоре, каде што наместо куќичката, или Марс, ги набљудуваме блиските ѕвезди, во однос на позадината каде што пак наместо планина, сега ги имаме поодалечените ѕвезди или галакси. Кога станува збор за ѕвездена паралакса не треба ние да се движеме на Земјата (како што беше и со случајот на мерење на паралкса на Марс), туку Земјата треба да се движи а ние, набљудувачите, да останеме на истото место. Во тој случај паралаксата би се забележала од исто место, но на различни датуми. За големи растојанија треба и самата основа на набљудување (во претходните примери растојанието на ливадата од неколку метри, односно растојанието од Парис до Француска Гвајана) да биде колку што е можно поголемо. Најголемото растојание кое што може да се искористи е растојанието на поголемиот дијаметар на елипсата опишана од Земјата при обиколката околу Сонцето. На пример, растојанието што Земјата го поминала од 1ви Јуни до 1ви Декември. За да набљудуваме паралакса треба да ја набљудуваме позицијата на некоја ѕвезда на овие два датуми. Ако позицијата на набљудуваната ѕвезда се менува во однос на нејзината позадина, значи имаме паралакса. Со ефектот на паралакса можеме и да го измериме растојанието помеѓу сонцето и набљудуваната ѕвезда. Но во универзумот има премногу ѕвезди кои можат да бидат потенцијални кандидати за мерење на паралакса, имајќи предвид дека во тоа време не се знаело за физичките карактеристики на ѕвездите.
Германскиот астроном кој тогаш работел во Русија, Вилхелм Штруве (Wilhelm Struve) развил критериуми за упростување на пронаоѓањето на ѕвезди како потенцијални кандидати за мерење на агол на паралакса добиен со привидното ѕвездено поместување. Тој предложил наместо бирање по случајност, да се направи фокусирање на ѕвезди кои според познати карактеристики имаат поголема веројатност да бидат поблиску до земјата. Некои од тие карактеристики биле привидната осветленост и сопственото движење на ѕвездите. Поблиските ѕвезди би имале поголем агол на паралакса и тој полесно ќе може да се забележи. Потоа бил развиен специјален тип на телескоп хелиометарот што овозможил многу попрецизни мерења и тоа конечно довело до првото официјално забележување на ѕвездена паралакса.
Во 1838 год. Фридрих Вилхелм Бесел за прв пат објавил релевантни податоци за мерења на паралакса на ѕвездата 61 Лебед (61 Cygni) во износ од 0.314 аглови секунди, што одговара на растојание од околу 10 светлосни години. Денес се знае дека ѕвездата 61 Лебед е бинарен ѕвезден систем со паралакса од 0.287 и 0.286 аглови секунди за секоја од ѕвездите. Овие мерења биле објавени кратко пред да се објават мерењата на Вега (Штруве) и Алфа Кентаури (Томас Хендерсон). Измерената паралакса на Вега била 0.261 аглови секунди, а моментално прифатената вредност е 0.130 аглови секунди, кореспондирајќи на 26 светлосни години. Измерената паралакса на Алфа Кентаури била 1 аголна секунда, а моментално прифатената е 0.755 и 0.797 аглови секунди за секоја од ѕвездите, затоа што денес се знае дека и Алфа Кенаури е бинарен ѕвезден систем. Алфа Кентаури и Проксима Кентаури кои го сочинуваат бинарниот ѕвезден систем се на растојание од 4 светлосни години и се најблиските ѕвезди до Сонцето, па со тоа имаат и најголема паралакса. Овие мерења се од исклучителна важност, затоа што освен добиените нови знаења за астрономските дистанци, истото води кон подобро калибрирање на опсервациите и за прв пат проценка на физичките параметри на ѕвездите како ѕвездена луминозност и големина.
Измерените агли на паралакса се екстремно мали. Една аголна секунда е еднаква на 1/3600 дел од еден аголен степен. За да се измери аголот на паралаксата на набљудуваната (блиската) ѕвезда, најпрво е потребно да се измери аголот (агол A) помеѓу таа ѕвезда и позадинската рефрентна ѕвезда, која што е ѕвезда без привидно движење, односно со паралакса од 0 степени. Најчесто тоа се ѕвезди или галаксии што се толку далеку што дури и со моќните телескопи изгледаат фиксни. Да претпоставиме дека измерениот агол A, помеѓу блиската и далечната ѕвезда е 1.5 аголни секунди. По шест месеци (половина од обиколката на Земјата околу Сонцето), го мериме истиот агол помеѓу истите две ѕвезди, агол B. Овој пат аголот е различен и изнесува 0.5 аголни секунди. Мерењето на аголот на паралакса може да се види на Слика 3 подолу. Двете црвени линии ја поврзуваат Земјата и далечната ѕвезда. Бидејќи ѕвездата е многу далечна линиите се паралелни. Двете црвени линии се на надворешната страна на триаголникот, па аголот на паралакса C е збирот од аголот А и аголот B, или 2 аголни секунди.
90° – А° + 90 – B° + C = 180°
-A° – B° + C° = 0
C° = A° + B°
Бидејќи аголот е екстремно мал можеме да кажеме дека триаголникот формиран на сликата е рамностран триаголник.
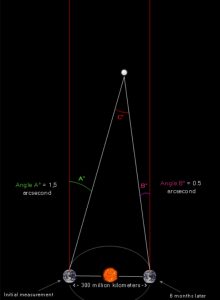
Слика 3
Ако повлечеме линија од врвот на триаголникот до средината на основата, триаголникот ќе го поделиме на два помали правоаголни триаголници, прикажано на Слика 4 (според едно од својствата на рамнокрак триаголник).
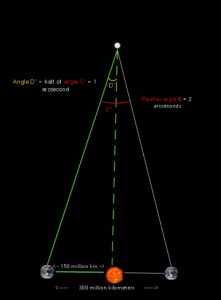
Слика 4
Кај правоаголните триаголници, користејќи тригонометрија, можеме да го најдеме растојанието од Сонцето до врвот на триаголникот, односно блиската ѕвезда. Тангенс од аголот D е резултатот од спротивната врз налегнатата страна. Според својствата на рамнокрак триаголник знаеме дека аголот D e половина од аголот C, односно 1 аголна секунда. 1 аголна секунда е 1/3600 аголен степен.
tan(1/3600) = 150.000.000/X
Значи растојанието, X, е еднакво на
X = 150.000.000/ tan(1/3600)
X = 3.1 *10 13
Значи ѕвездата што ја набљудуваме има агол на паралакса од 1 аголна секунда, односно 3,26 светлосни години, што соодвестува на астрономската единица од 1 парсек. 1 парсек е всушност растојанието од Сонцето до специфична ѕвезда кога таа има агол на паралакса од 1 аголна секунда, мерено од основа со 1 астрономска единица (150.000.000 km). Растојанијата до ѕвездите денес се мерат во парсеци или во светлосни години.
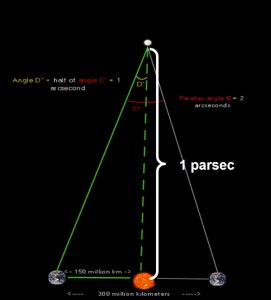
Слика 5
По првите мерења на ѕвездена паралакса направени се уште бројни други мерења на растојанијата до ѕвездите. Следно подобрување во инструментите за мерења на паралаксата се специјалните камери и фотографии со компјутерски програми кои го детектираат привидното поместување и лансирањето на телескопите во вселената. Сателитите Hipparcos (HIgh Precision PARallax COllecting Satellite), a потоа и Gaia и Hubble извршиле многу прецизни мерења на меѓуѕвездени растојанија користејќи паралакса. Со основа од 150.000.00 km може да се мери паралакса до 500 светлосни години. Меѓуѕвездените растојанија поголеми од 500 светлосни години се мерат по други принципи.
Користена литература: “The Astronomy Book: Big Ideas Simply Explained” Carole Stott, Robert Dinwiddie, David Hughes, Giles Sparrow
http://referenceframe.net/astronomy/how-astronomers-measure-distance-to-stars-using-parallax/
https://www.mccarthyobservatory.org/pdfs/pm020102.pdf
https://sci.esa.int/web/gaia/-/53197-seeing-and-measuring-farther